Подбор силовой установки для мотодельтаплана

Современный мотодельтаплан представляет собой новый вид легкого летательного аппарата - минисамолет с гибким крылом, примерная схема которого изображена на рис. 52. Обычно такой минисамолет характеризуется следующими параметрами [29]:

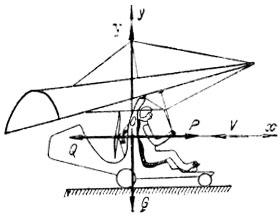
Рис. 52. Принципиальная схема мотодельтаплана

Подбор двигателя. Для удобства дальнейших рассуждений будем считать, что все силы, действующие на мотодельтаплан в случае установившегося горизонтального полета, приложены в ОЦТ; угол между вектором тяги двигателя и скоростью набегающего потока равен нулю. Тогда уравнение равновесия сил будет иметь вид

^* (Здесь и далее индексы "п" и "р" означают потребный и располагаемый соответственно.)

Из аэродинамики известно, что мощность потребная для преодоления силы сопротивления в горизонтальном полете,

Мощность, развиваемая силовой установкой,

где η_в - КПД винта. Для малых скоростей полета η_в = 0,3÷0,7, в первом приближении можно принять η_в = 0,5.

Если N_р = N_u, то мотодельтаплан летит горизонтально, в противном случае в зависимости от знака разности (N_p - N_u) он или снижается, или набирает высоту с вертикальной скоростью, пропорциональной величине этой разности:

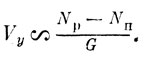
Проблема подбора двигателя заключается в нахождении оптимального значения мощности силовой установки. Из условия равновесия Y = G имеем 0,5C_yρV²S = G, следовательно, V = √(^2G/_(ρSCy)). Тогда N_п = √(^2G3/_(ρSCyK²)). Отсюда видно, что мощность, необходимая для осуществления горизонтального полета N_в, определяется главным образом весом аппарата и его аэродинамическим качеством. В том случае, если надо подсчитать тягу двигателя, необходимую для выполнения горизонтального полета, эта зависимость выступает еще яснее: P_п = ^G/_K.

Необходимо соизмерять мощность двигателя с полетным весом аппарата и без необходимости не увеличивать ее. В качестве контрольного критерия следует принять V_y.

Подбор воздушного винта. В качестве воздушного вин. та обычно используют двухлопастный высокооборотныц пропеллер диаметром 700-750 мм, развивающий тягу до 400 Н. К его достоинствам следует отнести простоту конструкции и малый вес, к недостаткам - значительные габариты и повышенную угрозу безопасности полета.

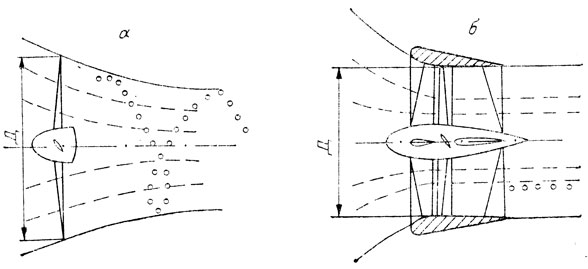
Рис. 53. Принцип работы движителей. а - воздушный винт (поток закручен); б - вентилятор (поток практически прямолинеен)

В качестве движителя может быть применен вентилятор. В отличие от винта закрученность вытекающих из вентилятора струй воздуха меньше (рис. 53). Поскольку эффективность вентилятора выше, при прочих равных условиях он имеет диаметр меньше, чем у винта. Основные недостатки вентилятора - трудности в проектировании и постройке.

Отунелованный винт - компромисс между винтом и вентилятором. Он позволяет реализовать преимущества каждого из них, избегая их недостатков.

М. Родзевич в работе [29] приводит алгоритм расчета геометрии отунелованного винта.

Алгоритм состоит из трех частей - А, Б, В. В первой методом последовательных приближений определяется КПД винта, во второй - угол установки лопасти в расчетном сечении, а также уточняются значения КПД и диаметра винта; в третьей - все основные параметры: тяга винта в полете, КПД в полете, скорость воздуха на входе в плоскость винта, углы атаки сечений но размаху лопасти, углы установки сечений по размаху лопасти. За расчетное принято сечение, отстоящее от оси вращения винта на 0,7 его радиуса.

Расчет проводится для предполагаемой скорости полета и для скорости взлета. В обоих случаях тяга винта должна быть не меньше той, которая необходима для полета. Перейдем к алгоритму.

А.

1. Задаем значение линейной скорости на конце лопасти U = ^πRn/₃₀.
2. Как уже говорилось, η_в = 0,3-0,7; принимаем в первом приближении какое-то значение КПД винта в указанном диапазоне.
3. Считаем, что полет мотодельтаплана проходит на высоте 500 м, где скорость звука в воздухе c = 338,2 ^м/_с; массовая плотность воздуха ρ = 1,18 ^кг/_м³. Определяем при этих условиях значение отношения ^U/_c.
4. Коэффициент ξ, входящий в формулу статической тяги винта, развиваемой на стенде, определяется зависимостью ξ = -0,2222 (^U/_c)² + 1.
5. Подсчитываем статическую тягу винта P_с = [2πρ(η_вξMU)²]^1/₃.
6. Определяем коэффициент k₁, необходимый для подсчета КПД винта в первом приближении: k₁ = ^2P_с/_(πρU²R²). πρНаходим КПД винта в первом приближении: η_В1 = -1220,2377k²₁ + 57,4999k₁ + 0,1354.

Как правило, полученное значение не будет равно исходному, принятому в п. 2. Поэтому берем значение η_в, переднее между полученным и исходным, и повторяем расчет во втором приближении. Делаем так несколько приближений до тех пор, пока полученное и исходное значения η_в практически не станут равными. Обычно для этого хватает 2-3 приближений.

Б.

1. Определяем угол установки лопасти в расчетном сечении: φ = 460,6724k₁ + 2,7, где k₁ берется из последнего приближения части А.
2. Подсчитываем величину λ = ^V/_U.
3. Уточняем значение коэффициента k: k₂ = 9,7296*10^-6φ + 0,13498λ.
4. Подсчитываем уточненное значение КПД винта: η_в = 1220,2377k²₂ + 57,4999k₂ + 0,1351.
5. Находим значение коэффициента k_d, исиользуемого при проверке линейной скорости концов лопастей:
   k_d = ^{k₂(λ + √(λ2 + k₂)}/_(2ηвξ),
   где λ определено в п. 9; k₂ - в п. 10; η_в - в п. 11; ξ - в п. 4.
6. Проверяем значение линейной скорости конца лопасти по формуле
   U = √(^2M/_πρkdR³),
   M = ^30N_в/_(πn).
7. Полученное значение U должно совпасть с исходным, принятым в п. 1. Если этого не произошло, следует взять значение U, среднее между исходным и полученным, и снова провести расчет по п. п. 9-14. Для получения приемлемых результатов обычно достаточно 2-3 приближений.

В.

1. Тяга винта в полете определяется по формуле P_р = 0,46315k₂U²D² = 1,85k₂U²R².
2. Окончательно определяем КПД винта в полете: η_в = ^P_рRV/_(MU) = ^0,5P_рV/_Nп.
3. Скорость воздуха в расчетном сечении винта W = 0,5(V + √(V² + ^0,54Р_р/_R²)).
4. Угол атаки в расчетном сечении α_0,7 = φ - arctg ^1,42857W/_U.
5. Подсчитываем углы установки сечений по размаху лопасти φ_x = α_0,7 + arctg ^W/_(Ux), x = ^r/_R.
6. Остается определить b_0,7 (хорда лопасти), b_0,7 = 0,785D²σ, где σ - коэффициент полноты.

Профили сечений можно отыскать в соответствующих справочниках.

Влияние силовой установки на устойчивость и управляемость мотодельтаплана. На устойчивость и управляемость мотодельтаплана влияют в основном три параметра силовой установки: вес, сила тяги, число оборотов.

Вес двигателя, находящегося не в общем центре тяжести системы крыло - двигатель - пилот, создает продольный момент M_дв = С_двa. Момент положителен, т. е. кабрирующий, если двигатель находится позади центра тяжести, или отрицателен, т. е. пикирующий, если двигатель впереди центра тяжести. Значение момента определяется весом двигателя и плечом, на котором этот вес приложен. Для уравновешивания момента в случае задней установки двигателя пилот должен переместиться вперед или назад в случае передней установки двигателя на расстояние, определяемое из условия Δt_дв = ^M_дв/_Gпил..

Когда вектор тяги не проходит через общий центр тяжести мотодельтаплана, тоже возникает продольный момент - пикирующий, если вектор тяги проходит выше центра тяжести, или кабрирующий, если вектор тяги проходит ниже центра тяжести. Значение момента определяется из выражения M_р = Р_рb, где b - плечо вектора тяги. Для уравновешивания этого момента пилот должен переместиться вперед при кабрирующем или назад при пикирующем моменте на расстояние, определяемое из условия Δt_р = ^M_р/_Cпил.

Кроме всего прочего, установка двигателя по высоте мотодельтаплана влияет на общую устойчивость полета. Чем ниже от плоскости крыла находится силовая установка, тем большую устойчивость приобретает полет, и наоборот.

Когда двигатель находится выше центра тяжести, необходимо подсчитать из условия балансировки пикирующего момента минимально допустимый вес пилота. В среднем для разных типов мотодельтапланов минимально допустимый вес пилота составляет примерно 50 кг.

Вектор тяги создает значительно больший продольный момент, чем вес силовой установки. Поэтому надо если не устранять, то хотя бы значительно уменьшать продольный момент от силы тяги. В пользу этого свидетельствует еще и то обстоятельство, что мотодельтаплан "должен выполнять как моторные полеты, так и планирующие. Переход из одного состояния полета в другое не должен сопровождаться возникновением чрезмерно больного продольного момента, создающего угрозу безопасности полета.

Величина момента крена, возникающего при работе двигателя и зависящего от мощности двигателя и числа ?оборотов, вычисляется по известной формуле:

Для парирования его пилот должен переместиться в сторону на расстояние, определяемое из условия

Обычно это очень небольшое расстояние, которое пилот может даже не почувствовать.

Общие требования к конструкции мотодельтаплана. Безусловно, на первый план следует выдвинуть безопасность полета на всех этапах, для чего:

• воздушный винт должен иметь эффективное ограждение и прочную фиксацию на аппарате;
• топливные бачки должны быть сконструированы так, чтобы в любой полетной ситуации не произошло выливания бензина на пилота или конструкцию;
• пилот должен иметь возможность без затруднений компенсировать моменты, возникающие от веса силовой установки и ее тяги;
• должна быть обеспечена необходимая прочность конструкции мотодельтаплана;
• аппарат должен быть оборудован основными аэронавигационными приборами: указателем скорости, указателем сноса, вариометром.