Расчет геометрии цилиндрического крыла

Ранее говорилось, что цилиндрическое крыло дельтаплана имеет значительное преимущество по аэродинамическому качеству перед обычным коническим крылом. Ирднако на практике такое крыло встречается редко, видимо, потому, что при кажущейся простоте изготовить его не так легко, как коническое. Сказываются тут, Конечно, и технологические трудности - каким способом гнуть трубы, не повредив их, как раскроить парус, учтя при этом разность длин материала по верхней и нижней сторонам паруса, и многое другое. Большинство затруднений упирается в неумение произвести несложные математические вычисления. Поэтому приведем методику вычисления основных геометрических параметров цилиндрического крыла, разработанную по просьбе автора сотрудником Экспериментального завода спортивной авиации (г. Пренай) Р. К. Диргелой.

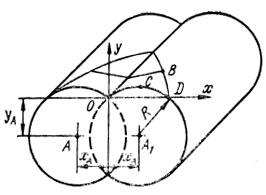
Рис. 49. К определению диаметров цилиндрических поверхностей, образующих крыло

Определение диаметра образующих крыло цилиндров. Пусть крыло дельтаплана образуется поверхностями цилиндров так, как показано на рис. 49. Килевая труба проходит по линии пересечения цилиндров, а любая точна паруса и боковой трубы находится на поверхности соответствующего цилиндра. Рассмотрим самый простой случай, когда киль аппарата прямой и точно совпадает с линией пересечения цилиндров, а боковые трубы и парус точно облегают поверхности цилиндров. Выберем систему координат xOy с началом в точке O, лежащей на линии пересечения цилиндров. Обозначим центры цилиндров через A и A₁, радиус - через R. Теперь можно перейти к расчетной части.

Уравнение окружности для произвольной точки C, находящейся на поверхности цилиндра, имеет вид

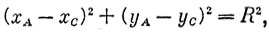
где x_A - известная величина; y_A - искомая величина; x_C и y_C - варьируемые параметры (обычно уже известны). Чтобы определить y_A, надо решить систему уравнений для трех точек, находящихся на поверхности цилиндра;

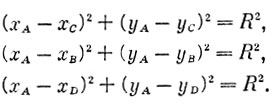
В результате получим величину y_A (промежуточные действия опущены, чтобы не загромождать текст). Теперь определим радиус цилиндра, образующего поверхность

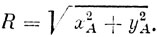
Расчет координат оси боковой трубы. Для простоты будем рассматривать только правую половину крыла. Пусть она образуется цилиндром радиусом R, который мы уже определили. Рассечем этот цилиндр плоскость под углом δ, равным половине угла при вершине дельтаплана. Тогда в сечении получим эллипс, большая полуось которого равна ^R/_{sin δ}, а малая-радиусу цилиндра R.

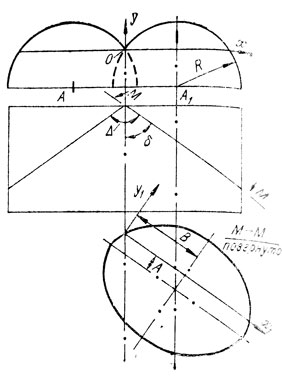
Рис. 50. К расчету координат оси боковой трубы

Систему координат берем ту же самую, но повернутую относительно исходной на тот же угол δ. При этом удаление начала координат по оси Ox от центра эллипса составит B, а по оси Oy равно A (рис. 50). Эти значения нетрудно снять с чертежа крыла.

Поскольку в сечении цилиндра мы получили эллипс, применительно к нашей системе координат можно записать уравнение эллипса в виде

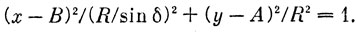
После преобразования получим искомое уравнение оси боковой трубы

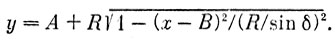
Остается подставить в него соответствующие значения x (поскольку все остальные величины известны). Получим абсолютные координаты оси боковой трубы.

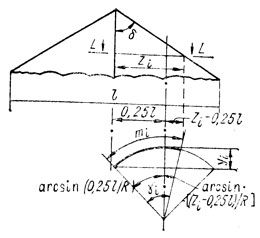
Рис. 51. К расчету раскроя паруса для цилиндрического крыла

Теоретический расчет раскроя паруса. Парус цилиндрического крыла не имеет купольности, поэтому в каждом сечении крыла, перпендикулярном килевой трубе, он будет представлен в виде дуги окружности, подсчитать величину которой не представляет трудности. На рис. 51 изображено такое сечение, отстоящее от килевой трубы или вершины крыла на z_i и имеющее на виде в плане хорду b. Из математики известно, что определить длину дуги можно, зная радиус окружности и угол, под которым эта дуга видна из центра окружности. Чтобы не производить громоздких геометрических построений для определения угла дуги, воспользуемся аналитической зависимостью, вытекающей из рис. 51:

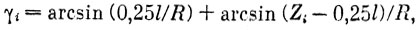
где угол γ_i - в радианах. Теперь, зная из предыдущих вычислений радиус цилиндра R и определив для ряда сечений величину угла γ_i, легко подсчитать длины дуг окружностей в соответствующих сечениях крыла, перпендикулярных килевой трубе:

Величина m_i не учитывает диаметра труб. Поэтому при раскрое материала для пошива паруса необходимо давать припуск на трубу.