Боковая устойчивость

В результате внешнего воздействия дельтаплан может выйти из режима исходного полета и начать так называемое боковое возмущенное движение. Устойчивость дельтаплана в боковом движении называется боковой устойчивостью. Экспериментальные исследования боковой устойчивости дельтаплана были проведены в Варшавском техническом университете [14]. В аэродинамической трубе продувался дельтаплан класса "Стандарт", имеющий угол при вершине 80° и купольность 5° на сторону. Цилиндр постоянной плотности, имитирующий пилота, имел массу 80 кг. Крыло рассматривалось как жесткое тело. Боковое движение аппарата и его устойчивость изучались при изменении скорости набегающего потока, положения пилота (горизонтальное, вертикальное) и общего центра тяжести относительно крыла. Перемещения дельтаплана описывались в обычной правосторонней системе координат. Боковые возмущения движения считались малыми.

При указанных условиях были получены безразмерные уравнения движения, практически не отличающиеся от аналогичных уравнений движения для обычных планеров. Ввиду сложности эти уравнения здесь не приводятся. Скажем только, что три из них описывают углы скольжения, крена и рысканья, а два других представляют собой кинематические соотношения. Характеристическое уравнение этой системы уравнений может быть представлено в виде

где λ, является оператором дифференцирования. Не принимая во внимание корень λ = 0, получим, что данное характеристическое уравнение имеет в общем случае два действительных и два комплексных корня:

Отсюда следует, что боковое движение дельтаплана будет устойчивым, если действительная часть корня ζ_i имеет отрицательные значения. Если при этом значения мнимой части корня η_i отличны от нуля, начинается боковое колебательное движение с частотой v.

Для бокового возмущенного движения во всем диапазоне значений λ определены отношения начальных величин углов скольжения β, крена γ, рысканья -φ и значений ω_x и ω_y к (β² + γ² + ω_x² + ω_y²,)^0,5 (рис. 14).

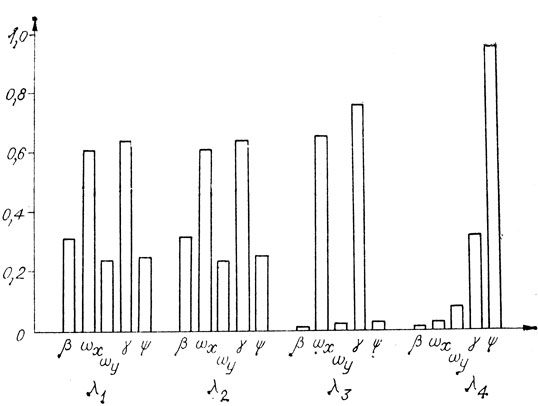
Рис. 14. Значения модулей компонентов, входящих в λ_i, λ_1,2 = -0,16477±0,93797; λ₃ = -0,86241; λ₄ = -0,08103.

Во всех исследованных случаях два корня из четырех имели небольшие отрицательные действительные части и были комплексными, а два других - действительными, отрицательными и существенно разными по модулю (см. рис. 14).

Теоретический анализ показывает, что рассматриваемый дельтаплан после возмущения бокового движения выполняет следующие асимметричные движения:

• быстро затухающее боковое колебание, включающее рысканье, крен и скольжение (это боковое колебание известно как датский шаг) и соответствующее паре комплексных корней;
• быстро затухающее апериодическое вращение, известное как вид крена и отвечающее большому действительному отрицательному корню;
• медленно затухающее апериодическое движение крепа и рысканья, известное как спиральное движение и соответствующее малому действительному отрицательному корню.

Обычно затухание колебаний датского шага возрастает с увеличением расстояния между крылом и общим цент ром тяжести (из-за увеличения момента инерции), а также с повышением скорости полета (из-за возрастания так называемой аэродинамической жесткости). Влияние этих факторов зависит от позиции пилота - вертикальной и горизонтальной. Если положение пилота вертикальное, затухание непостоянно при высоких скоростях полета, особенно когда общий центр тяжести находится близко к крылу (короткая подвесная система). Это, кроме всего прочего, является одной из причин развития флаттерного пикирования. Отмечается, что при горизонтальном положении пилота проблема затухания датского шага практически исчезает.

Затухание апериодического вращения возрастает при тех же условиях - удалении общего центра тяжести от крыла и повышении скорости полета дельтаплана - и может уменьшаться лишь в случае очень короткой подвесной системы и вертикального положения пилота.

Сказанное о затухании первых двух видов колебаний верно и для апериодического спирального движения, только здесь меньше влияние положения пилота.

Теоретический анализ боковой устойчивости дельтаплана класса "Стандарт" показал, что аппарат устойчив при обычных скоростях полета. Его боковая устойчивость существенно зависит от расстояния между общим центром тяжести и плоскостью каркаса крыла и меньше - от положения пилота. Высота полета не оказывает большого влияния на характеристики возмущенного бокового движения дельтаплана, зато может оказать заметное влияние сильное изменение аэродинамических характеристик крыла вследствие гибкости труб каркаса и развития колебаний на задней кромке паруса.

В экспериментах была обнаружена практически линейная зависимость коэффициентов бокового движения от угла скольжения β в диапазонах угла атаки, обычно используемых при полетах. На этом основании в работе [3] предлагаются эмпирические зависимости для расчета коэффициентов:

где m^β_x0, m^β_y0 даны при λ = 2,58; d^- = 0,03.

Зависимости дают приемлемые результаты для крыльев с λ = 1,5÷3,5; d^- = 0,034÷0,18; f^- = 0,25÷1,00; χ = 20÷60°; v = 0÷15°.

Аэродинамика парусного крыла

Парусное крыло, разработанное в 1948 г. в США, сочетает высокие летные характеристики с простотой складывающейся конструкции. Иногда его называю) мембранным крылом. Оно состоит из жесткой передней кромки (обычно трубчатого лонжерона) и жестких про филированных концевых нервюр (рис. 15). Задняя кромка образуется тросом, натянутым между нервюрами. Необходимо, чтобы в полете очертания задней кромки менялись как можно меньше. Для этого задают предварительное натяжение троса задней кромки, величина которого определяется в процессе проектирования. Предварительное натяжение можно существенно уменьшить, увеличив число нервюр или применив какое-либо устройство для поддержания задней кромки. Поверхность парусного крыла - ткань, туго обернутая вокруг передней кромки и закрепленная на заднем тросе. Применяете ткань, мало изменяющая свои линейные размеры под действием внешних условий.

Устойчивость формы парусного крыла в отличие от гибкого обеспечивается в основном натяжением паруса. Поэтому оно может работать как при положительных так и отрицательных углах атаки, хотя при коэффициенте подъемной силы C_y = 0 возможно возникновение не устойчивости поверхности крыла [24]. На аэродинамику парусного крыла оказывают значительное влияние угол атаки и скорость полета, предварительное натяжении ткани паруса и троса задней кромки, упругость конструкции.

В полете воздушная нагрузка уравновешивается упругим прогибом крыла и дополнительным индуктивным натяжением ткани паруса и троса задней кромки (см рис. 15). Из рисунка видно, что при α = 0 профиль крыла симметричен, а с увеличением угла атаки возникаем кривизна профиля, увеличивающаяся с ростом α. Аэродинамический эффект такого явления эквивалентен эффекту автоматического закрылка крыла. Благодаря ему крыло имеет очень мягкий срыв потока на критических углах атаки, в результате чего полет сменяется крутым, но медленным снижением. В этом режиме аппарат инертен по рысканью.

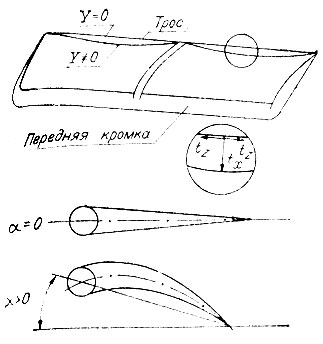
Рис. 15. Внешний вид и принцип работы парусного крыла

Если углы поперечного V малы, парусное крыло имеет тенденцию к скольжению во время крена. Угол поперечного V порядка 8⁰ устраняет это явление. Желательно концевые сечения крыла закрутить на малый отрицательный угол -до 2-3° [24].

Парусное крыло по своим аэродинамическим характеристикам сравнимо с жестким (рис. 16). Более гибкие крылья имеют меньшее удлинение, что вызывается стремлением уменьшить, эффекты деформации. Кривая C_y = f(α) парусного крыла идет вверх более круто, чем жесткого (см. рис. 4). Это вызывается эффектами упругости паруса [24].

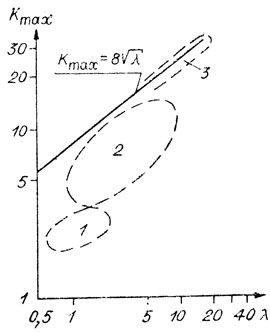
Рис. 16. Зависимость K_max крыльев разного типа от их удлинения. Сплошная линия относится к жесткому крылу. 1 - аппараты с гибким крылом (дельтапланы); 2 - с полужестким крылом; 3 - с парусным крылом

Для топкого мембранного профиля крыла в работе [23] приводится следующая зависимость коэффициента подъемной силы от угла атаки и степени натяжения паруса:

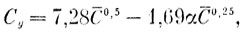
где C = ^{(c - b)}/_b. Здесь c - длина дужки профиля; b - хорда профиля.

Подсчитать коэффициенты подъемной силы C_y для всего парусного крыла значительно сложнее. По данным работы [24],

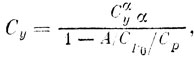
где A - аэродинамический фактор, учитывающий эластичность парусного крыла; C_P0 = ^2P₀/_(ρV²S) - коэффициент предварительного натяжения троса заднем кромки (для текущего значения C_y); C_p - дивергенция коэффициента предварительного натяжения троса для теоретического случая C^α_y→∞.

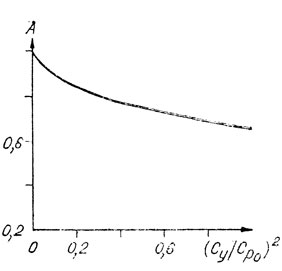
Рис. 17. Зависимость аэродинамического параметра А от (^C_y/_Cp0)²

На рис. 17 приведена зависимость аэродинамического фактора A от величины (^C_y/^C_p0)² для экспериментального крыла [24], имеющего следующие параметры: λ = 5; β = 0,16 - параметр формы задней кромки; R₀ = 3, R_E = 0,3, N_T = 0,008 (числа Стиффнесса). Здесь R₀ характеризует отношение предварительного натяжения паруса по размаху крыла к предварительному напряжению его по хорде; R_e = ^E_T/_(EαS^0,5), где E - соответствующий модуль упругости; N_T = ^P₀/_(ETS^0,5), где P₀ - предварительное натяжение троса задней кромки; β = ^lt_x/_(4P0), где t_x - натяжение паруса по хорде.

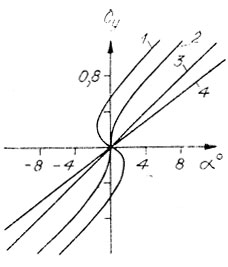
Рис. 18. Влияние скорости полета на теоретические кривые C_y = f(α) парусного крыла. ^C_p0/_Cp = 0,5 (1); 1,0 (2), 4,0 (2); 4 - жесткое крыло

На рис. 18 приведена зависимость коэффициента подъемной силы парусного крыла от угла атаки для разным значений отношения ^C_p0/_Cp. При низких скоростях полета или большом предварительном натяжении троса задней кромки C_P>>C_P и кривая C_y = f(α) становится линейной, как для жесткого крыла. При высокой скорости полета или слабом предварительном натяжении троса C_P0 = C_P и начальный наклон кривой C_y = f(α) стремится к бесконечности. Но тут вступает в действие аэродинамический параметр A, вызывающий с увеличением скорости полета более сильное натяжение паруса. В результате кривая подъемной силы начинает выпрямляться и при больших углах атаки стабилизируется.

В работе 124] указывается, что предварительное натяжение троса задней кромки должно быть:

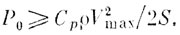
В то же время на околосрывных режимах необходимо соблюдать условие:

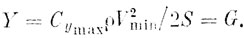
Поделив первое равенство на второе, имеем

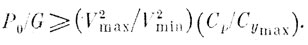
Отсюда получим, что при срыве потока для типичного отношения ^C_P/_Cymax = 0,5 предварительное натяжение троса задней кромки должно быть не меньше половины полетного веса аппарата [24].

Дельтаплан с парусным крылом может иметь аэродинамическое качество порядка 15-20. По сути дела, это сверхлегкий балансирный планер с крылом изменяемой кривизны. Для него может быть применено балансирное продольное управление и аэродинамическое по крену и направлению. По статической устойчивости и управляемости аппарат будет мало отличаться от планера с жестким крылом. Такой дельтаплан можно использовать не только для полетов в Динамических потоках, но и для перелетов в термических потоках.